Елементи комбінаторики, теорії ймовірностей і математичної статистики. 11 клас
Елементи комбінаторики, теорії ймовірностей і математичної статистики from russoua
Задача 4.1 У коробці шість однакових кубиків, які занумеровані числами від 1 до 6. По одному витягають усі кубики. Знайдіть імовірність того, що номери витягнутих кубиків з'являться у порядку зростання.
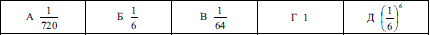 Розв'язання: В теорії ймовірностей на задачах з комбінаторики побудовані всі складні теореми і виведення формул, тому хто добре розбереться з простими задачами – Комбінаторика, як і сама Теорія ймовірності не складна.
Розв'язання: В теорії ймовірностей на задачах з комбінаторики побудовані всі складні теореми і виведення формул, тому хто добре розбереться з простими задачами – Комбінаторика, як і сама Теорія ймовірності не складна.
Для прикладу, проаналізуємо дану задачу – кубик з цифрою 1 можна витягнути в 1 із 6 варіантів, тобто ймовірність першим витягнути кубик з цифрою 1 рівна 1/6. Після цього залишиться 5 кубиків з номерами від 2 до 5. Ймовірність з цієї кількості витягнути кубик з номером 2 рівна 1/5. Відповідно, ймовірність вибрати третій з цифрою 3 – 1/4 і так далі.
Сумарна ймовірність витягнути кубики в порядку зростання рівна добутку ймовірностей
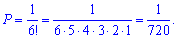
Ймовірність 1/720 відповідає варіанту А тестових відповідей.
Відповідь: А.
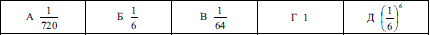 Розв'язання: В теорії ймовірностей на задачах з комбінаторики побудовані всі складні теореми і виведення формул, тому хто добре розбереться з простими задачами – Комбінаторика, як і сама Теорія ймовірності не складна.
Розв'язання: В теорії ймовірностей на задачах з комбінаторики побудовані всі складні теореми і виведення формул, тому хто добре розбереться з простими задачами – Комбінаторика, як і сама Теорія ймовірності не складна.Для прикладу, проаналізуємо дану задачу – кубик з цифрою 1 можна витягнути в 1 із 6 варіантів, тобто ймовірність першим витягнути кубик з цифрою 1 рівна 1/6. Після цього залишиться 5 кубиків з номерами від 2 до 5. Ймовірність з цієї кількості витягнути кубик з номером 2 рівна 1/5. Відповідно, ймовірність вибрати третій з цифрою 3 – 1/4 і так далі.
Сумарна ймовірність витягнути кубики в порядку зростання рівна добутку ймовірностей
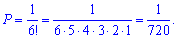
Ймовірність 1/720 відповідає варіанту А тестових відповідей.
Відповідь: А.
Задача 4.2 (Т-07, 33) З натуральних чисел від 1 до 30 учень навмання називає одне. Яка ймовірність того, що це число є дільником числа 30?
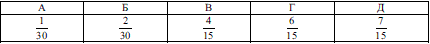 Розв'язання: Аналізуємо умову – задано 30 чисел, випишемо в ряд дільники числа 30.
Розв'язання: Аналізуємо умову – задано 30 чисел, випишемо в ряд дільники числа 30.
1;2;3;5;6;10;15;30.Їх кількість рівна 8
N=8.
Щоб знайти ймовірність ділимо кількість сприятливих подій до загальної кількості можливих
P=8/30=4/15.Отримана відповідь наведена в варіанті В ЗНО тестів, і може добавити 1 бал на тестуванні.
Відповідь: В.
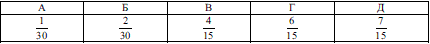 Розв'язання: Аналізуємо умову – задано 30 чисел, випишемо в ряд дільники числа 30.
Розв'язання: Аналізуємо умову – задано 30 чисел, випишемо в ряд дільники числа 30.1;2;3;5;6;10;15;30.Їх кількість рівна 8
N=8.
Щоб знайти ймовірність ділимо кількість сприятливих подій до загальної кількості можливих
P=8/30=4/15.Отримана відповідь наведена в варіанті В ЗНО тестів, і може добавити 1 бал на тестуванні.
Відповідь: В.
Задача 4.3 У коробці лежать різнокольорові кульки, з яких 40 - червоні, 20 - коричневі, а всі, що залишилися - жовті. З'ясуйте, скільки жовтих кульок лежить у коробці, якщо ймовірність вибору випадковим чином жовтої кульки дорівнює 0,75.
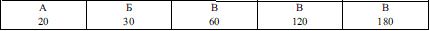 Розв'язання: До прикладу з комбінаторики потрібно скласти рівняння. Ймовірність витягнути жовту кульку серед N всіх кульок рівна
Розв'язання: До прикладу з комбінаторики потрібно скласти рівняння. Ймовірність витягнути жовту кульку серед N всіх кульок рівна
P(A)=0,75.
Кількість червоних і коричневих рівна
40+20=60.
З іншої сторони ця ймовірність обчислюється з рівняння
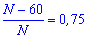
Розв'язавши його, ми знайдемо загальну кількість кульок, а також зможемо обчислити кількість жовтих
N-60=0,75*N;
N(1-0,75)=60;
0,25*N=60;
N=60/0,25=240 – кількість усіх кульок.
Далі обчислюємо скільки серед знайдених жовтих
n=N-60=240-60=180.
Результат відповідає варіанту Д ЗНО тестів.
Відповідь: Д.
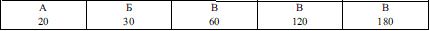 Розв'язання: До прикладу з комбінаторики потрібно скласти рівняння. Ймовірність витягнути жовту кульку серед N всіх кульок рівна
Розв'язання: До прикладу з комбінаторики потрібно скласти рівняння. Ймовірність витягнути жовту кульку серед N всіх кульок рівнаP(A)=0,75.
Кількість червоних і коричневих рівна
40+20=60.
З іншої сторони ця ймовірність обчислюється з рівняння
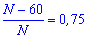
Розв'язавши його, ми знайдемо загальну кількість кульок, а також зможемо обчислити кількість жовтих
N-60=0,75*N;
N(1-0,75)=60;
0,25*N=60;
N=60/0,25=240 – кількість усіх кульок.
Далі обчислюємо скільки серед знайдених жовтих
n=N-60=240-60=180.
Результат відповідає варіанту Д ЗНО тестів.
Відповідь: Д.
Задача 4.4 (Т-06, 31) Власник банкоматної картки забув останні дві цифри свого РІN-коду, але пам'ятає, що вони різні. Знайдіть імовірність того, що з першої спроби він отримає доступ до системи.
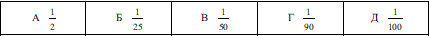 Розв'язання: Міркування для обчислення наступні: варіантів правильно визначити першу цифру 10, тобто числа від 0 до 9. Другу цифру, оскільки вони різні, можна вибрати 9 способами. Загальна кількість комбінацій рівна
Розв'язання: Міркування для обчислення наступні: варіантів правильно визначити першу цифру 10, тобто числа від 0 до 9. Другу цифру, оскільки вони різні, можна вибрати 9 способами. Загальна кількість комбінацій рівна
N=10*9=90.Тоді імовірність становить
P=1/N=1/90.
Помилку в подібних задачах роблять ті, хто не враховує нуля до кількості чисел. Тоді ймовірність рівна
P=1/(9*8)=1/72
Але це помилкові міркування, тому для себе запам'ятайте цей момент. До речі, навіть тестові відповіді не містять значення 1/72.
Попередньо знайдена відповідь відповідає варіанту Г.
Відповідь: Г.
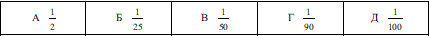 Розв'язання: Міркування для обчислення наступні: варіантів правильно визначити першу цифру 10, тобто числа від 0 до 9. Другу цифру, оскільки вони різні, можна вибрати 9 способами. Загальна кількість комбінацій рівна
Розв'язання: Міркування для обчислення наступні: варіантів правильно визначити першу цифру 10, тобто числа від 0 до 9. Другу цифру, оскільки вони різні, можна вибрати 9 способами. Загальна кількість комбінацій рівнаN=10*9=90.Тоді імовірність становить
P=1/N=1/90.
Помилку в подібних задачах роблять ті, хто не враховує нуля до кількості чисел. Тоді ймовірність рівна
P=1/(9*8)=1/72
Але це помилкові міркування, тому для себе запам'ятайте цей момент. До речі, навіть тестові відповіді не містять значення 1/72.
Попередньо знайдена відповідь відповідає варіанту Г.
Відповідь: Г.
Задача 4.5 Задано цифри 1; 2; 3; 4; 5; 6. З них утворюють всі можливі шестицифрові числа, використовуючи кожну цифру тільки один раз. Знайдіть імовірність того, що взяте навмання одне з цих чисел ділитиметься на 5.
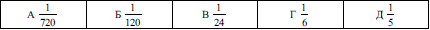 Розв'язання: Кількість престановок з 6 цифер рівна факторіалу чисел, тобто 6!. Якщо взяте навмання число ділиться на 5, то остання цифра рівна 5, а попередні приймають значення 1, 2, 3, 4 , 6.Їх кількість =5, тому з них можна скласти 5 факторіал різних чисел, що діляться на 5.
Розв'язання: Кількість престановок з 6 цифер рівна факторіалу чисел, тобто 6!. Якщо взяте навмання число ділиться на 5, то остання цифра рівна 5, а попередні приймають значення 1, 2, 3, 4 , 6.Їх кількість =5, тому з них можна скласти 5 факторіал різних чисел, що діляться на 5.
Звідси ймовірність рівна частці факторіалів
P=5!/6!=1/6.
Значення відповідає варіанту Г.
Відповідь: Г.
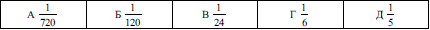 Розв'язання: Кількість престановок з 6 цифер рівна факторіалу чисел, тобто 6!. Якщо взяте навмання число ділиться на 5, то остання цифра рівна 5, а попередні приймають значення 1, 2, 3, 4 , 6.Їх кількість =5, тому з них можна скласти 5 факторіал різних чисел, що діляться на 5.
Розв'язання: Кількість престановок з 6 цифер рівна факторіалу чисел, тобто 6!. Якщо взяте навмання число ділиться на 5, то остання цифра рівна 5, а попередні приймають значення 1, 2, 3, 4 , 6.Їх кількість =5, тому з них можна скласти 5 факторіал різних чисел, що діляться на 5.Звідси ймовірність рівна частці факторіалів
P=5!/6!=1/6.
Значення відповідає варіанту Г.
Відповідь: Г.
Задача 4.6 Задано цифри 2; 3; 4; 5; 6. Знайдіть кількість непарних п'ятицифрових чисел, які можна скласти із цифр, використовуючи кожну цифру тільки один раз.
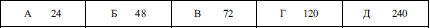 Розв'язання: Запишемо, які із заданих чисел непарні 3, 5.
Розв'язання: Запишемо, які із заданих чисел непарні 3, 5.
Попередні 4 цифри можна змінювати, тобто отримувати комбінації 2 типів
abcd3, abcd5.
Сумарна кількість таких чисел рівна 4 факторіал помножити на 2
4!*2= 4*3*2*1*2=6*8=48.
Кількість відповідає варіанту Б тестових відповідей.
Відповідь: Б.
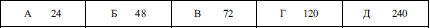 Розв'язання: Запишемо, які із заданих чисел непарні 3, 5.
Розв'язання: Запишемо, які із заданих чисел непарні 3, 5.Попередні 4 цифри можна змінювати, тобто отримувати комбінації 2 типів
abcd3, abcd5.
Сумарна кількість таких чисел рівна 4 факторіал помножити на 2
4!*2= 4*3*2*1*2=6*8=48.
Кількість відповідає варіанту Б тестових відповідей.
Відповідь: Б.
Задача 4.7 Середній вік учнів одного класу дорівнює 16 років. Обчисліть середній вік цих учнів через рік.
 Розв'язання: Досить простий приклад, можливо навіть важко його віднести до комбінаторики. Розв'язок отримаємо простим сумуванням
Розв'язання: Досить простий приклад, можливо навіть важко його віднести до комбінаторики. Розв'язок отримаємо простим сумуванням
16+1=17 років.
Відповідь: Г.
 Розв'язання: Досить простий приклад, можливо навіть важко його віднести до комбінаторики. Розв'язок отримаємо простим сумуванням
Розв'язання: Досить простий приклад, можливо навіть важко його віднести до комбінаторики. Розв'язок отримаємо простим сумуванням16+1=17 років.
Відповідь: Г.
Задача 4.8 Скількома різними способами можна скласти трикольоровий прапор з горизонтальними смугами заданої ширини (див. рис.), якщо є тканина шести різних кольорів?

 Розв'язання: Розпишемо всі можливі комбінації кольорів прапора.
Розв'язання: Розпишемо всі можливі комбінації кольорів прапора.
Перший колір можна вибрати 6 способами, другий – на одиницю менше 5 (оскільки один колір вже вибрали) і третій – 4 способами. Кількість способів обчислюємо множенням варіантів вибору усіх трьох смуг прапора
6*5*4=30*4=120.
За такою схемою обчислюють подібні задачі комбінаторики.
Відповідь: В.

 Розв'язання: Розпишемо всі можливі комбінації кольорів прапора.
Розв'язання: Розпишемо всі можливі комбінації кольорів прапора.Перший колір можна вибрати 6 способами, другий – на одиницю менше 5 (оскільки один колір вже вибрали) і третій – 4 способами. Кількість способів обчислюємо множенням варіантів вибору усіх трьох смуг прапора
6*5*4=30*4=120.
За такою схемою обчислюють подібні задачі комбінаторики.
Відповідь: В.
Задача 4.9 У квадраті зі стороною 4 см відмічають точку. Яка імовірність того, що відстань від цієї точки до найближчої сторони квадрата менше 1 см?
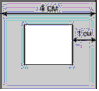
 Розв'язання: Маємо геометричну задачу на ймовірність. Все що потрібно для обчислення ймовірності – це площу заштрихованої частини квадрата розділити на площу всього квадрата. Обчислимо площі
Розв'язання: Маємо геометричну задачу на ймовірність. Все що потрібно для обчислення ймовірності – це площу заштрихованої частини квадрата розділити на площу всього квадрата. Обчислимо площі
S= 4^2=16;
2*2=4;
S1=16-4=8.
Далі знаходимо ймовірність діленням відповідних площ
P=8/16=1/2.
Результат відповідає варіанту Г ЗНО тестів.
Відповідь: Г.

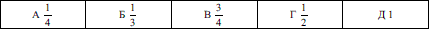 Розв'язання: Маємо геометричну задачу на ймовірність. Все що потрібно для обчислення ймовірності – це площу заштрихованої частини квадрата розділити на площу всього квадрата. Обчислимо площі
Розв'язання: Маємо геометричну задачу на ймовірність. Все що потрібно для обчислення ймовірності – це площу заштрихованої частини квадрата розділити на площу всього квадрата. Обчислимо площіS= 4^2=16;
2*2=4;
S1=16-4=8.
Далі знаходимо ймовірність діленням відповідних площ
P=8/16=1/2.
Результат відповідає варіанту Г ЗНО тестів.
Відповідь: Г.
В Задачах 4.10 - 4.11 правильна відповідь оцінюється 2 балами.
Задача 4.10 Учаснику телевізійного шоу дозволяється відімкнути довільні два сейфи із п'яти запропонованих (у двох із них лежать призи, а інші - порожні). Обчисліть ймовірність отримання двох призів.
Розв'язання: Ймовірність відкрити першим сейф з призом рівна 2/5, оскільки маємо в 2 призи, а всього 5 сейфів. Після цього, чисто теоретично, залишається 4 сейфи і 1 приз, тобто ймовірність вгадати 2 сейф рівна 1/4. Сумарна ймовірність взяти обидва призи за теоремою про сумування ймовірностей рівна їх добутку
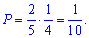
Значення 0,1 дає надію, що кожен 10 учасник телевізійного шоу може «зірвати банк».
Відповідь: 0,1.
Розв'язання: Ймовірність відкрити першим сейф з призом рівна 2/5, оскільки маємо в 2 призи, а всього 5 сейфів. Після цього, чисто теоретично, залишається 4 сейфи і 1 приз, тобто ймовірність вгадати 2 сейф рівна 1/4. Сумарна ймовірність взяти обидва призи за теоремою про сумування ймовірностей рівна їх добутку
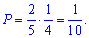
Значення 0,1 дає надію, що кожен 10 учасник телевізійного шоу може «зірвати банк».
Відповідь: 0,1.
Задача 4.11 Середній вік одинадцяти футболістів команди становить 22 роки. Під час гри одного з футболістів було вилучено з поля, після чого середній вік гравців, що залишилися, став 21 рік. Скільки років футболісту, який залишив поле? (Т-07, 26)
Розв'язання: Багатьом може здатися, що завдання складне, але це не так. Давайте міркувати так: в футбольній команді одинадцять граків.
Помножимо середній вік на кількість футболістів і ми будемо знати сумарно роки гравців всієї команди
11*22=242.
Після вилучення одного гравця їх кількість дорівнює 10.
За наведеною ж схемою визначаємо вік 10 гравців, враховуючи, що їх середній вік 21 рік.
10*21=210.
Різниця між знайденими значеннями і є віком гравця, що залишив поле
242-210=32 (роки).
Після обчислень задача багатьом здається зовсім не важкою, хоча на тестах її віднесли до складних.
Відповідь: 32.
Розв'язання: Багатьом може здатися, що завдання складне, але це не так. Давайте міркувати так: в футбольній команді одинадцять граків.
Помножимо середній вік на кількість футболістів і ми будемо знати сумарно роки гравців всієї команди
11*22=242.
Після вилучення одного гравця їх кількість дорівнює 10.
За наведеною ж схемою визначаємо вік 10 гравців, враховуючи, що їх середній вік 21 рік.
10*21=210.
Різниця між знайденими значеннями і є віком гравця, що залишив поле
242-210=32 (роки).
Після обчислень задача багатьом здається зовсім не важкою, хоча на тестах її віднесли до складних.
Відповідь: 32.



Коментарі
Дописати коментар