Правила диференціювання

Теорія:

Теорема 1.

Якщо функції y=f(x) і y=g(x) мають похідну в точці x, тоді і їх сума має похідну в точці x, причому похідна суми дорівнює сумі похідних:

(f(x)+g(x))′=f′(x)+g′(x)

Теорема 2.

Якщо функція y=f(x) маює похідну в точці x, тоді і функція y=kf(x) має похідну в точці x, причому:

(kf(x))′=kf′(x)

Теорема 3.

Якщо функції y=f(x) і y=g(x) мають похідну в точці x, тоді і їх добуток має похідну в точці x, причому:

(f(x)g(x))′=f′(x)⋅g(x)+f(x)⋅g′(x)

На практиці цю теорему формулюють так:

похідна добутку двох функцій дорівнює сумі двох доданків; перший доданок є добуток похідної першої функції на другу функцію, а другий доданок є добуток першої функції на похідну другої функції.

Якщо функції y=f(x) і y=g(x) мають похідну в точці x і в цій точці g(x)≠0, тоді і функція y=f(x)g(x) має похідну в точці x, причому:

(f(x)g(x))′=f′(x)⋅g(x)−f(x)⋅g′(x)g2(x)

(k1u+k2v)'=k1u'+k2v'(uv)'=u'v+uv'(uv)'=u'v−uv'v2

Приклад:

u=x2v=sinx1.(2x2−3sinx)'=2(x2)'−3(sinx)'=2⋅2x−3cosx=4x−3cosx2.(x2sinx)'=(x2)'sinx+x2(sinx)'=2xsinx+x2cosx3.(x2sinx)'=(x2)'sinx−x2(sinx)'(sinx)2=2xsinx−x2cosxsin2x

Похідна складеної функції

Нехай функція 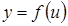 визначена в деякому околі точки  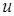і функція  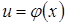визначена в деякому околі точки 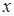, таким чином визначена складена функція .

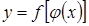Теорема 3.3. Якщо функція 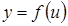 має похідну в точці  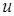і функція  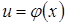має похідну в точці 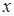, то складена функція  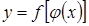також має похідну в точці 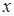, причому

,                              (3.6)

або скорочено

                                         (3.6*)

Приклад. Знайти похідну функції .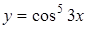

Розв’язання. Приймаючи 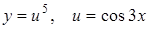, маємо:

Тут враховано, що 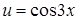 також складена функція і тому за формулою (3.6) вона має похідну .

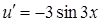Таблиця похідних основних елементарних функцій

(Table of Derivative Formulas)

	1)		;
	2)		,		(, або  при );
	3)		,		();
	4)		;
	5)		,		();
	6)		,		();
	7)		;
	8)		;
	9)		,		();
10)		,		();
11)		,		();
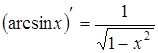12)		,		();
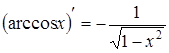13)		;
14)		;